Pythagoreans, Math, Music and Geometry | Early European History And Religion

Home | Category: Science and Nature / Philosophy

PYTHAGOREANS AND PYTHAGORAS

Pythagoras

The Pythagoreans were followers of the philosopher-mathematician Pythagoras. Headquartered first on the island of Samos and later Croton in southern Italy, they were the first to make the profound discovery that all aspects of nature — musical notes, mathematics, science, architecture and engineering — followed rules that were determined by the relationship between numbers.

The Pythagoreans were like an ascetic religious cult. They believed in reincarnation and conducted purification rituals that attempted to erase wrongs committed in past lives. They were required to follow many rules. They had to be vegetarians. They couldn't drink wine and were required to observe periods of silence. Their purification rituals were conducted with great secrecy.

Pythagoras of Samos (sixth century B.C.) is said to have been the first man to call himself a philosopher and is credited with coining the word philosophy. None of his original writings survive. According to legend he fled the Aegean island of Samos as a youth to escape from an evil tyrant. After being exposed to new ideas in Egypt and Asia Minor he established a school in the Italian colony of Kroton in 530 B.C. After being persecuted and forced to flee again he settled in Metapontum, Greece, where he died around 500 B.C.

There is no evidence that Pythagoras was a mathematician, let alone proved the theorem named after him or discovered the ratios of musical intervals. He was however a number-worshiper and a guru who founded a commune and spoke of the coming of a messiah-like figure. The theorem named after him (“the sum of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides”) was known to the Sumerians as early as 2000 B.C.

Pythagoras and Arithmetic

Proclus (A.D. 412-485) wrote: "So Pythagoras turned geometrical philosophy into a form of liberal education by seeking its first principles in a higher realm of reality...." [Source: Proclus In Eucl. p. 65 Friedlander]

“In his treatise on Arithmetic, Aristoxenus said that Pythagoras was the first to carry that study beyond the needs of commerce, and his statement is confirmed by everything we otherwise know. By the end of the fifth century B.C. we find that there is a widespread interest in such subjects and that these are studied for their own sake. Now this new interest cannot have been wholly the work of a school; it must have originated with some great man, and there is no one but Pythagoras to whom we can refer it. As, however, he wrote nothing, we have no sure means of distinguishing his own teaching from that of his followers in the next generation or two. All we can safely say is that, the more primitive any Pythagorean doctrine appears, the more likely it is to be that of Pythagoras himself, and all the more so if it can be shown to have points of contact with views which we know to have been held in his own time or shortly before it. In particular, when we find the later Pythagoreans teaching things that were already something of an anachronism in their own day, we may be pretty sure we are dealing with survivals which only the authority of the master's name could have preserved. Some of these must be mentioned at once, though the developed system belongs to a later part of our story. It is only by separating its earliest form from its later that the place of Pythagoreanism in Greek thought can be made clear, though we must remember that no one can now pretend to draw the line between its successive stages with any certainty. [Source: John Burnet (1863-1928), “Early Greek Philosophy” London and Edinburgh: A. and C. Black, 1892, 3rd edition, 1920, Evansville University ]

Pythagoras and Euclid

“One of the most remarkable statements we have about Pythagoreanism is what we are told of Eurytus on the unimpeachable authority of Archytas. Eurytus was the disciple of Philolaus, and Aristoxenus mentioned him along with Philolaus as having taught the last of the Pythagoreans, the men with whom he himself was acquainted. He therefore belongs to the beginning of the fourth century B.C., by which time the Pythagorean system was fully developed, and he was no eccentric enthusiast, but one of the foremost men in the school. We are told of him, then, that he used to give the number of all sorts of things, such as horses and men, and that he demonstrated these by arranging pebbles in a certain way. Moreover, Aristotle compares his procedure to that of those who bring numbers into figures (schêmata) like the triangle and the square.

“Now these statements, and especially the remark of Aristotle last quoted, seem to imply the existence at this date, and earlier, of a numerical symbolism quite distinct from the alphabetical notation on the one hand and from the Euclidean representation of numbers by lines on the other. The former was inconvenient for arithmetical purposes, because the zero was not yet invented. The representation of numbers by lines was adopted to avoid the difficulties raised by the discovery of irrational quantities, and is of much later date. It seems rather that numbers were originally represented by dots arranged in symmetrical and easily recognized patterns, of which the marking of dice or dominoes gives us the best idea. And these markings are, in fact, the best proof that this is a genuinely primitive method of indicating numbers; for they are of unknown antiquity, and go back to the time when men could only count by arranging numbers in such patterns, each of which became, as it were, a fresh unit.

“It is, therefore, significant that we do not find any clue to what Aristotle meant by "those who bring numbers into figures like the triangle and the square" till we come to certain late writers who called themselves Pythagoreans, and revived the study of arithmetic as a science independent of geometry. These men not only abandoned the linear symbolism of Euclid, but also regarded the alphabetical notation, which they did use, as inadequate to represent the true nature of number. Nicomachus of Gerasa says, expressly that the letters used to represent numbers are purely conventional. The natural thing would be to represent linear or prime numbers by a row of units, polygonal numbers by units arranged so as to mark out the various plane figures, and solid numbers by units disposed in pyramids and so forth.

“Now it ought to be obvious that this is no innovation. Of course the employment of the letter alpha to represent the units is derived from the conventional notation; but otherwise we are clearly in presence of something which belongs to the very earliest stage of the science. We also gather that the dots were supposed to represent pebbles (psêphoi), and this throws light on early methods of what we still call calculation.

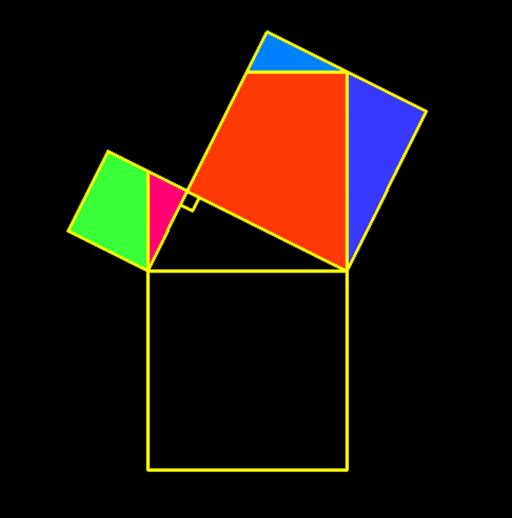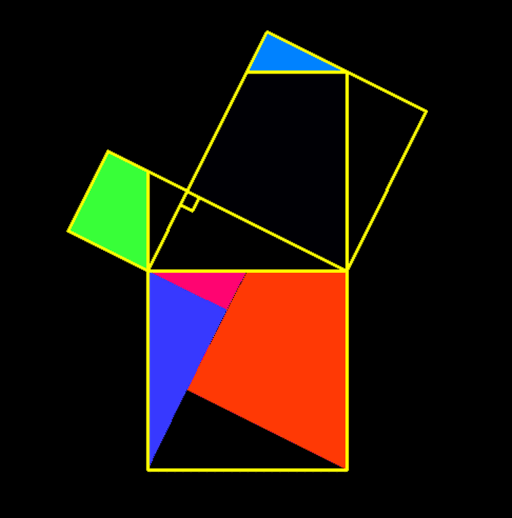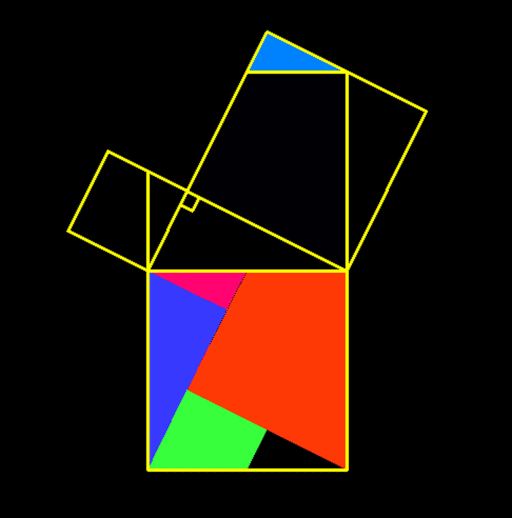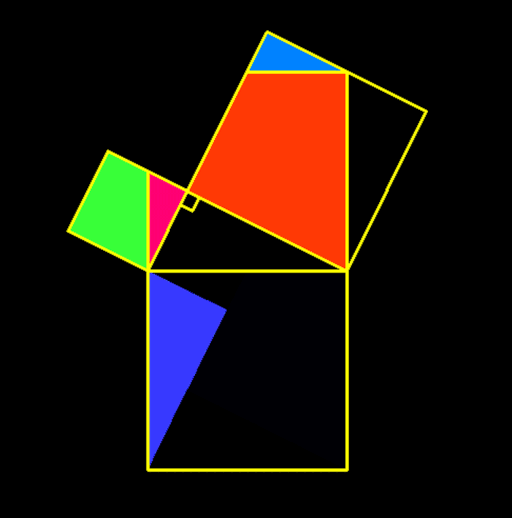
Pythagorean Theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. [Source Wikipedia]

The theorem can be written as an equation relating the lengths of the sides a, b and the hypotenuse c, sometimes called the Pythagorean equation: a² + b² = c²

The theorem is named for the Greek philosopher Pythagoras and has been proved numerous times by many different methods — possibly the most for any mathematical theorem. The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years.

Even though the formalized Pythagorean rule is what students are taught in school experts have long known that the Greeks inherited mathematical teachings from Egyptians, and the Egyptians in turn from the Babylonians. See Below

article/entry-1028.html#chapter-9"> africame.factsanddetails.com

Pythagoreans, Music and Things Are Numbers

"The Pythagoreans, according to Aristoxenus, practiced the purification (catharsis) of the body by medicine, and of the soul by music." [Source: Cramer, Paris Anthology I. 172]

The Pythagoreans showed how numbers could be used to describe the harmonies and beauties of music and introduced the musical terminology of the octave, the fifth, the forth, expressed as 2:1, 3:1 and 4:3. They found that the most pleasant sounds occurred in exact proportions and discovered that the length of a musical string was is in an exact numerical relation to the pitch of its tone.

Notes are sound waves created by vibrations. A vibration that is twice as high as another is an octave. Others that are pleasant together are those whose vibration are a forth or fifth higher. These same proportions are used in designing what are regarded as aesthetically pleasing building, which is why architecture has been called “frozen music."

The Pythagoreans argued that of numbers worked so well describing music they could also describe everything in the universe. Describing the Pythagoreans in his Metaphysics , Aristotle wrote: "they say that the things themselves are Numbers and do not place the objects of mathematics between Forms and sensible things...Since, again, they saw that the modifications and the ratios of the musical scales were expressible in numbers — since, then, all other things seemed in their whole nature, they supposed the elements of numbers to be the elements of all things, and the whole heaven to be a musical scale and a number...and the whole arrangement of the heavens they collected and fitted into their scheme; and if there was a gap anywhere, they readily made additions so as to make their whole theory coherent."

“It was this, no doubt, that led Pythagoras to say all things were numbers. We shall see that, at a later date, the Pythagoreans identified these numbers with geometrical figures; but the mere fact that they called them "numbers," taken in connection with what we are told about the method of Eurytus, is sufficient to show this was not the original sense of the doctrine. It is enough to suppose that Pythagoras reasoned somewhat as follows. If musical sounds can be reduced to numbers, why not everything else? There are many likenesses to number in things, and it may well be that a lucky experiment, like that by which the octave was discovered, will reveal their true numerical nature. The Neopythagorean writers, going back in this as in other matters to the earliest tradition of the school, indulge their fancy in trading out analogies between things and numbers in endless variety; but we are fortunately dispensed from following them in these vagaries. Aristotle tells us distinctly that the Pythagoreans explained only a few things by means of numbers, which means that Pythagoras himself left no developed doctrine on the subject, while the Pythagoreans of the fifth century did not care to add anything of the sort to the tradition. Aristotle does imply, however, that according to them the "right time" (kairos) was seven, justice was four, and marriage three. These identifications, with a few others like them, we may safely refer to Pythagoras or his immediate successors; but we must not attach too much importance to them. We must start, not from them, but from any statements we can find that present points of contact with the teaching of the Milesian school. These, we may fairly infer, belong to the system in its most primitive form. [Source: John Burnet (1863-1928), “Early Greek Philosophy” London and Edinburgh: A. and C. Black, 1892, 3rd edition, 1920, Evansville University ]

Pythagorean Numbers and Elements

Pythagoreans of Socrates time adapted Pythagorean ideas about numbers to the new theory of "elements." This is what makes it necessary to take up the consideration of the system once more in connexion with the pluralists. When the Pythagoreans returned to Southern Italy, they would find views prevalent there which demanded a partial reconstruction of their own system. We do not know that Empedocles founded a philosophical society, but there can be no doubt of his influence on the medical school of these regions; and we also know now that Philolaus played a part in the history of medicine. This gives us the clue to what formerly seemed obscure. The tradition is that the Pythagoreans explained the elements as built up of geometrical figures, a theory we can study for ourselves in the more developed form it attained in Plato's Timaeus. If they were to retain their position as the leaders of medical study in Italy, they were bound to account for the elements. [Source: John Burnet (1863-1928), “Early Greek Philosophy” London and Edinburgh: A. and C. Black, 1892, 3rd edition, 1920, Evansville University ]

“We must not take it for granted, however, that the Pythagorean construction of the elements was exactly the same as that we find in Plato's Timaeus. As we have seen, there is good reason for believing they only knew three of the regular solids, the cube, the pyramid (tetrahedron), and the dodecahedron. Now Plato makes Timaeus start from fire and earth, and in the construction of the elements he proceeds in such a way that the octahedron and the icosahedron can easily be transformed into pyramids, while the cube and the dodecahedron cannot. From this it follows that, while air and water pass readily into fire, earth cannot do so, and the dodecahedron is reserved for another purpose, which we shall consider presently. This would exactly suit the Pythagorean system; for it would leave room for a dualism of the kind outlined in the Second Part of the poem of Parmenides. We know that Hippasus made Fire the first principle, and we see from the Timaeus how it would be possible to represent air and water as forms of fire. The other element is, however, earth, not air, as we have seen reason to believe that it was in early Pythagoreanism. That would be a natural result of the discovery of atmospheric air by Empedocles and of his general theory of the elements. It would also explain the puzzling fact, which we had to leave unexplained above, that Aristotle identifies the two "forms" spoken of by Parmenides with Fire and Earth.

“The most interesting point in the theory is, however, the use made of the dodecahedron. It was identified, we are told, with the "sphere of the universe," or, as it is put in the Philolaic fragment, with the "hull of the sphere." Whatever we may think of the authenticity of the fragments, there is no reason to doubt that this is a genuine Pythagorean expression, and it must be taken in close connection with the word "keel" applied to the central fire. The structure of the world was compared to the building of a ship, an idea of which there are other traces. The key to what we are told of the dodecahedron is also given by Plato. In the Phaedo, which must have been written before the doctrine of the regular solids was fully established, we read that the "true earth," if looked at from above, is "many-colored like the balls that are made of twelve pieces of leather."

Pythagoreans and Triangular, Square and Oblong Numbers

Aetius (A.D. 394- 454) wrote: "Ten is the very nature of number. All Greeks and all barbarians alike count up to ten, and having reached ten revert again to the unity. And again, Pythagoras maintains, the power of the number 10 lies in the number 4, the tetrad. This is the reason: if one starts at the unit (1) and adds the successive number up to 4, one will make up the number 10 (1+2+3+4 = 10). And if one exceeds the tetrad, one will exceed 10 too.... So that the number by the unit resides in the number 10, but potentially in the number 4. And so the Pythagoreans used to invoke the Tetrad as their most binding oath: "By him that gave to our generation the Tetractys, which contains the fount and root of eternal nature...'" [Source: Aetius I. 3.8]

“That Aristotle refers to this seems clear, and is confirmed by the tradition that the great revelation made by Pythagoras to mankind was precisely a figure of this kind, the tetraktys, by which the Pythagoreans used to swear, and we have the authority of Speusippus for holding that the whole theory was Pythagorean. In later days there were many kinds of tetraktys, but the original one, that by which the Pythagoreans swore, was the "tetraktys of the dekad." It represented the number ten as the triangle of four.

“It showed at a glance that 1 + 2 + 3 + 4 = 10. Speusippus tells us of several properties which the Pythagoreans discovered in the dekad. It is, for instance, the first number that has in it an equal number of prime and composite numbers. How much of this goes back to Pythagoras himself, we cannot tell; but we are probably justified in referring to him the conclusion that it is "according to nature" that all Hellenes and barbarians count up to ten and then begin over again. [Source: John Burnet (1863-1928), “Early Greek Philosophy” London and Edinburgh: A. and C. Black, 1892, 3rd edition, 1920, Evansville University ]

“It is obvious that the tetraktys may be indefinitely extended so as to exhibit the sums of the series of successive integers in a graphic form, and these sums are accordingly called "triangular numbers." For similar reasons, the sums of the series of successive odd numbers are called "square numbers," and those of successive even numbers "oblong." If odd numbers are added in the form of gnomons, the result is always a similar figure, namely a square, while, if even numbers are added, we get a series of rectangles. It is clear, then, that we are entitled to refer the study of sums of series to Pythagoras himself; but whether he went beyond the oblong, and studied pyramidal or cubic numbers, we cannot say.

Geometry, Harmonics, Incommensurability and Proportion

“It is easy to see how this way of representing numbers would suggest problems of a geometrical nature. The dots which stand for the pebbles are regularly called "boundary-stones" (horoi, termini, "terms"), and the area they mark out is the "field" (chôra). This is evidently an early way of speaking, and may be referred to Pythagoras himself. Now it must have struck him that "fields" could be compared as well as numbers, and it is likely that he knew the rough methods of doing this traditional in Egypt, though certainly these would fail to satisfy him. Once more the tradition is helpful in suggesting the direction his thoughts must have taken. He knew, of course, the use of the triangle 3, 4, 5 in constructing right angles. We have seen (§ XI) that it was familiar in the East from a very early date, and that Thales introduced it to the Hellenes, if they did not know it already. In later writers it is actually called the "Pythagorean triangle." Now the Pythagorean proposition par excellence is just that, in a right-angled triangle, the square on the hypotenuse is equal to the squares on the other two sides, and the so-called Pythagorean triangle is the application of its converse to a particular case. The very name "hypotenuse" (hupoteinousa) affords strong confirmation of the intimate connection between the two things. It means literally "the cord stretching over against," and this is surely just the rope of the "arpedonapt." It is, therefore, quite possible that this proposition was really discovered by Pythagoras, though we cannot be sure of that, and though the demonstration of it which Euclid gives is certainly not his. [Source: John Burnet (1863-1928), “Early Greek Philosophy” London and Edinburgh: A. and C. Black, 1892, 3rd edition, 1920, Evansville University ]

music of the spheres

“One great disappointment, however, awaited him. It follows at once from the Pythagorean proposition that the square on the diagonal of a square is double the square on its side, and this ought surely to be capable of arithmetical expression. As a matter of fact, however, there is no square number which can be divided into two equal square numbers, and so the problem cannot be solved. In this sense, it may be true that Pythagoras discovered the incommensurability of the diagonal and the side of a square, and the proof mentioned by Aristotle, namely, that, iff they were commensurable, we should have to say that an even number was equal to an odd number, is distinctly Pythagorean in character. However that may be, it is certain that Pythagoras did not care to pursue the subject any further. He may have stumbled on the fact that the square root of two is a surd, but we know that it was left for Plato's friends, Theodorus of Cyrene and Theaetetus, to give a complete theory of irrationals. For the present, the incommensurability of the diagonal and the square remained, as has been said, a "scandalous exception." Our tradition says that Hippasus of Metapontum was drowned at sea for revealing this skeleton in the cupboard.

“These last considerations show that, while it is quite safe to attribute the substance of the early books of Euclid to the early Pythagoreans, his arithmetical method is certainly not theirs. It operates with lines instead of with units, and it can therefore be applied to relations which are not capable of being expressed as equations between rational numbers. That is doubtless why arithmetic is not treated in Euclid till after plane geometry, a complete inversion of the original order. For the same reason, the doctrine of proportion which we find in Euclid cannot be Pythagorean, and is indeed the work of Eudoxus. Yet it is clear that the early Pythagoreans, and probably Pythagoras himself, studied proportion in their own way, and that the three "medieties" (mesotêtes) in particular go back to the founder, especially as the most complicated of them, the "harmonic," stands in close relation to his discovery of the octave. If we take the harmonic proportion 12:8:6, we find that 12:6 is the octave, 12:8 the fifth, and 8:6 the fourth, and it can hardly be doubted that Pythagoras himself discovered these intervals. The stories about his observing the harmonic intervals in a smithy, and then weighing the hammers that produced them, or suspending weights corresponding to those of the hammers to equal strings, are, indeed, impossible and absurd; but it is sheer waste of time to rationalize them. For our purpose their absurdity is their chief merit. They are not stories which any Greek mathematician could possibly have invented, but popular tales bearing witness to the existence of a real tradition that Pythagoras was the author of this momentous discovery. On the other hand, the statement that he discovered the "consonances" by measuring the lengths corresponding to them on the monochord is quite credible and involves no error in acoustics.

Pythagorean Soul: a "Harmony"

“The view that the soul is a "harmony," or rather an attunement, is intimately connected with the theory of the four elements. It cannot have belonged to the earliest form of Pythagoreanism; for, as shown in Plato's Phaedo, it is quite inconsistent with the idea that the soul can exist independently of the body. It is the very opposite of the belief that "any soul can enter any body." On the other hand, we are told in the Phaedo that it was accepted by Simmias and Cebes, who had heard Philolaus at Thebes, and by Echecrates of Phlius, who was the disciple of Philolaus and Eurytus. The account of the doctrine given by Plato is quite in accordance with the view that it was of medical origin.

Simmias says: "Our body being, as it were, strung and held together by the warm and the cold, the dry and the moist, and things of that sort, our soul is a sort of temperament and attunement of these, when they are mingled with one another well and in due proportion. If, then, our soul is an attunement, it is clear that, when the body has been relaxed or strung up out of measure by diseases and other ills, the soul must necessarily perish at once." This is clearly an-application of the theory of Alcmaeon (§ 96), and is in accordance with the views of the Sicilian school. It completes the evidence that the Pythagoreanism of the end of the fifth century was an adaptation of the old doctrine to the new principles introduced by Empedocles.

“It is further to be observed that, if the soul is regarded as an attunement in the Pythagorean sense, we should expect it to contain the three intervals then recognized, the fourth, the fifth and the octave, and this makes it extremely probable that Posidonius was right in saying that the doctrine of the tripartite soul, as we know it from the Republic of Plato, was really Pythagorean. It is quite inconsistent with Plato's own view of the soul, but agrees admirably with that just explained.

Image Sources: Wikimedia Commons

Text Sources: Internet Ancient History Sourcebook: Greece sourcebooks.fordham.edu ; Internet Ancient History Sourcebook: Hellenistic World sourcebooks.fordham.edu ; BBC Ancient Greeks bbc.co.uk/history/; Canadian Museum of History, Perseus Project - Tufts University; perseus.tufts.edu ; MIT Classics Online classics.mit.edu ; Gutenberg.org, Metropolitan Museum of Art, National Geographic, Smithsonian magazine, New York Times, Washington Post, Live Science, Discover magazine, Natural History magazine, Archaeology magazine, The New Yorker, Encyclopædia Britannica, "The Discoverers" and "The Creators" by Daniel Boorstin. "Greek and Roman Life" by Ian Jenkins from the British Museum, Wikipedia, Reuters, Associated Press, The Guardian, AFP and various books and other publications.

Last updated September 2024